MTH30: Precaulculus Mathematics

Textbook
Zoom
- Notes from Zoom meetings
Departmental Webpages
Exams and Quizes
Trig notes
Graphs of Trigonometric Functions
- Sine
- Cosine
- Tangent
- Secant
- Cotangent
Material from older classes
- Notes
- Homework Sets

Textbook

Our textbook is Precalculus by Jay Abramson, OpenStax

Zoom

Thursdays we meet online via zoom.

Zoom Link: Nikos Apostolakis MTH 30 Class
Meeting ID: 839 5829 9375
Passcode: 319493

Notes from Zoom meetings

Departmental Webpages

Exams and Quizes

Midterm Exam The answers: Solutions for the midterm
Third Quiz The answers: Solutions for third quiz
Fourth Quiz The answers: Solutions for fourth quiz
Fifth Quiz The answers: Solutions for fifth quiz
Sixth Quiz The answers: Solutions for sixth quiz

Trig notes

The definitions and basic identities of trigonometric functions: Trigonometric identites
Notes on Trigonometric Equations: Trigonometric Equations

Graphs of Trigonometric Functions

Sine

For an arc $\theta$ in the unit circle starting at the point $(0,1)$, $\sin \theta$ is the $y$-coordinate of its end point. The following animation shows the graph traced as the endpoint traverses the unit circle:

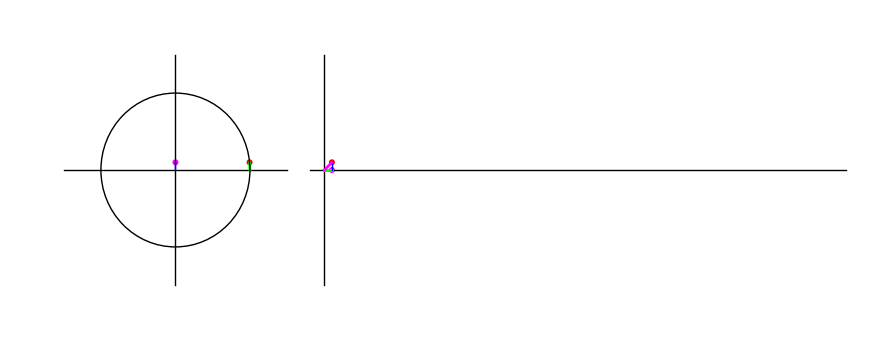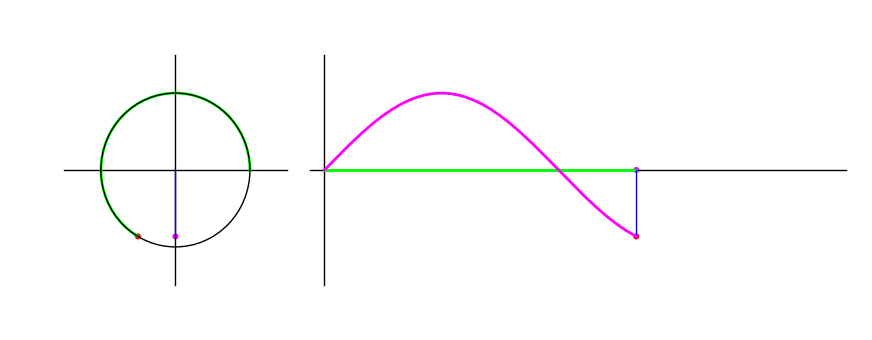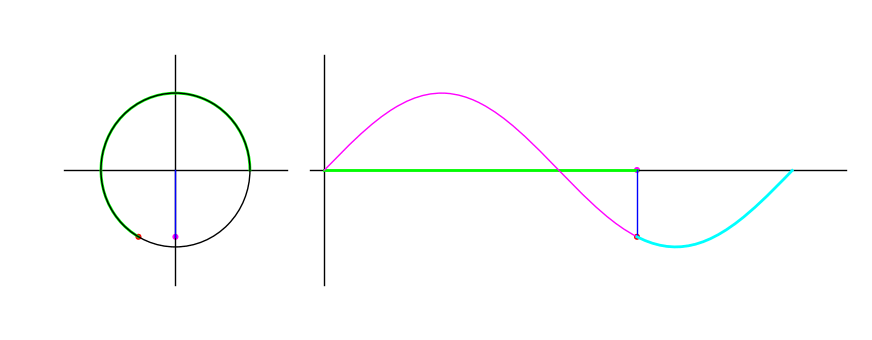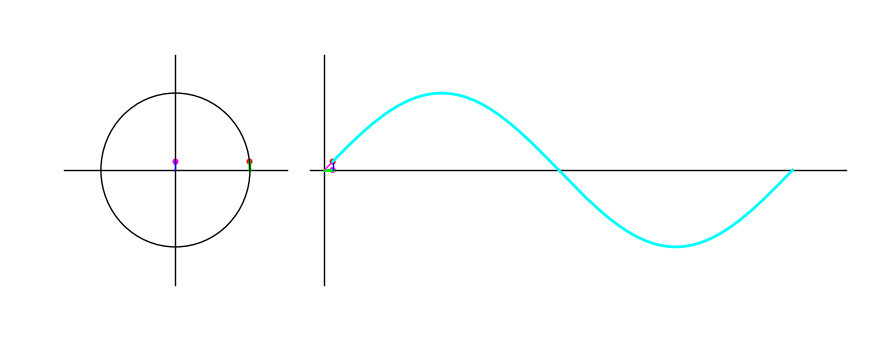
Figure 1: The sine of a point moving in a circle

Cosine

$\cos \theta$ is the $x$-coordinate of the end point. The following animation shows the graph traced as the endpoint traverses the unit circle:

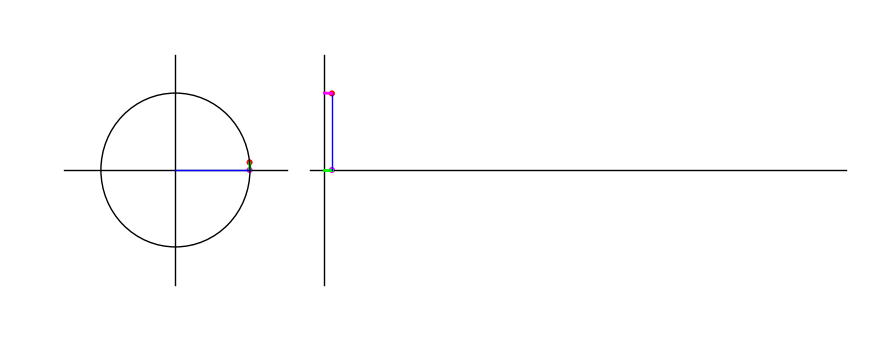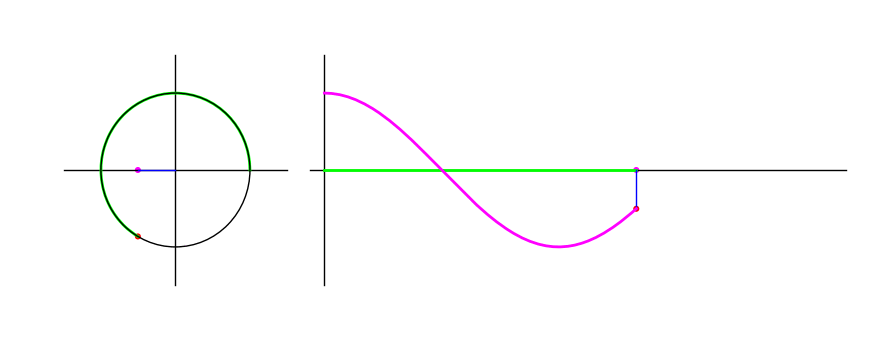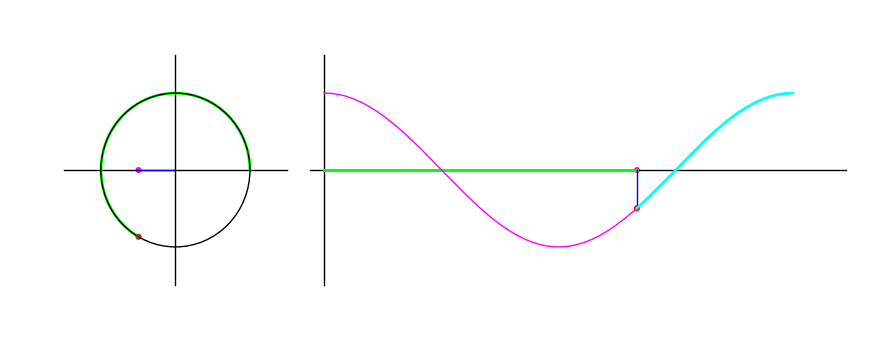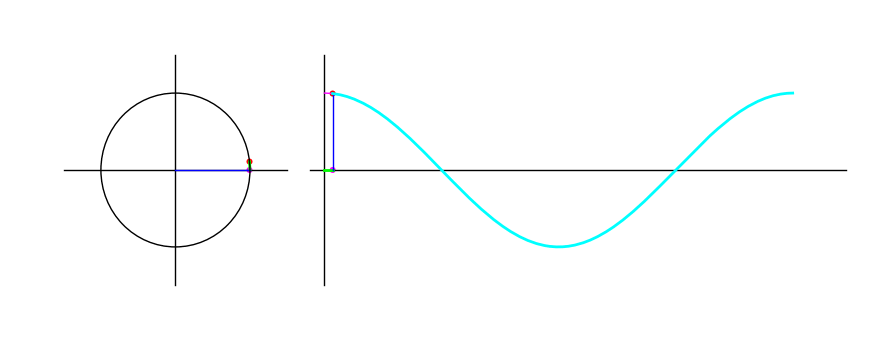
Figure 2: The cosine of a point moving in a circle

Tangent

$\tan \theta$ is the signed distance of interscetion of the radius through the endpoint and the line tangent to the circle at the point $(0,1)$. The following animation shows the graph traced as the endpoint traverses the unit circle:

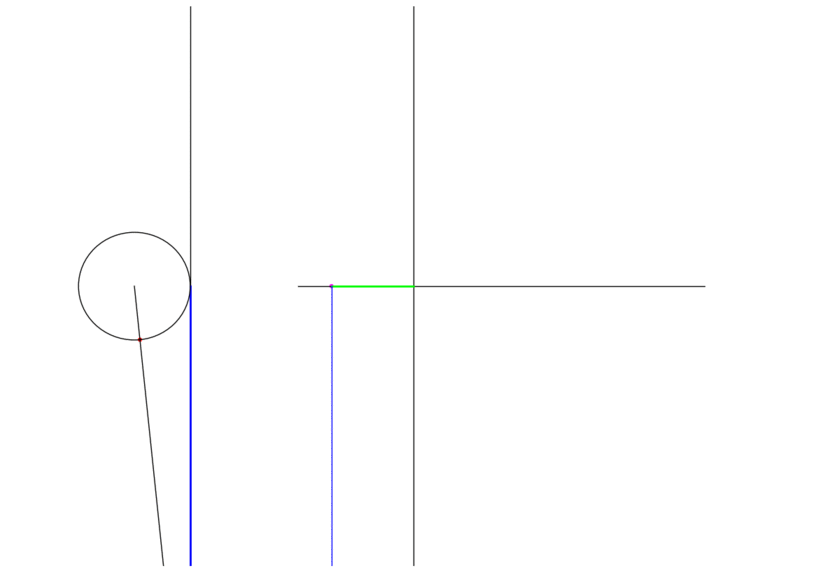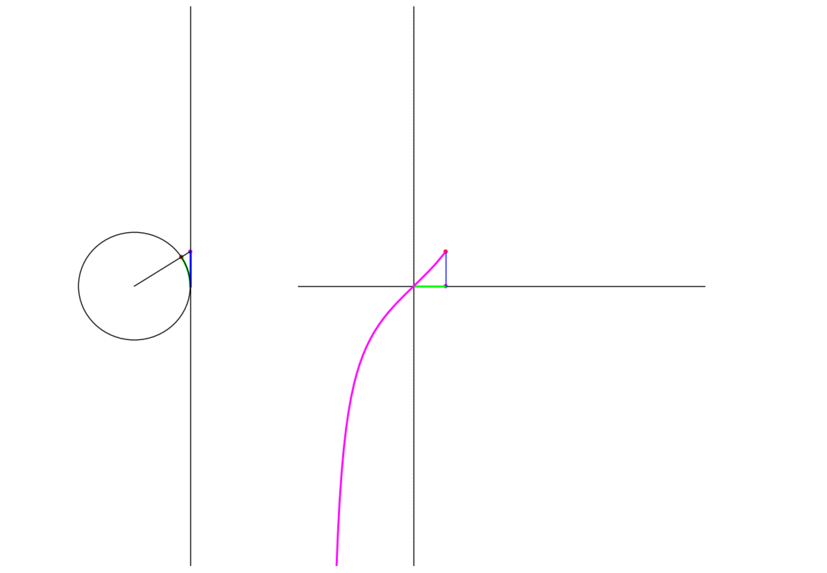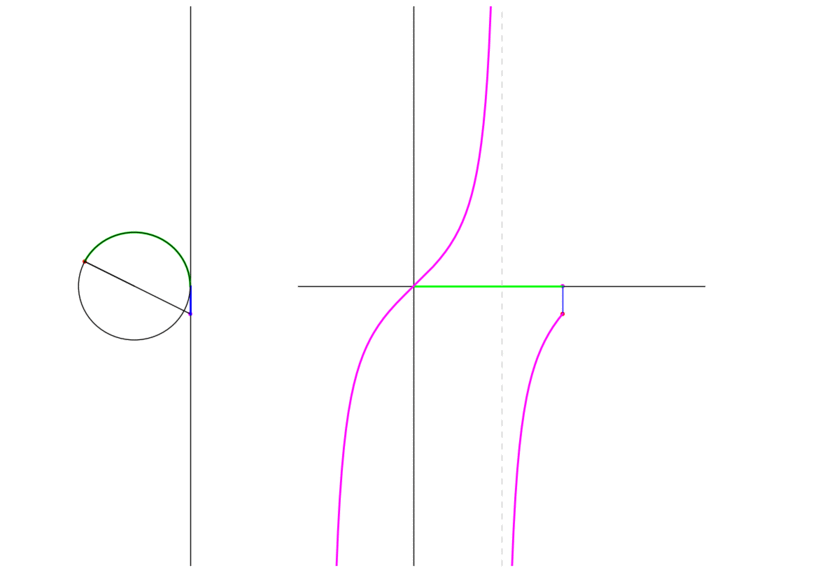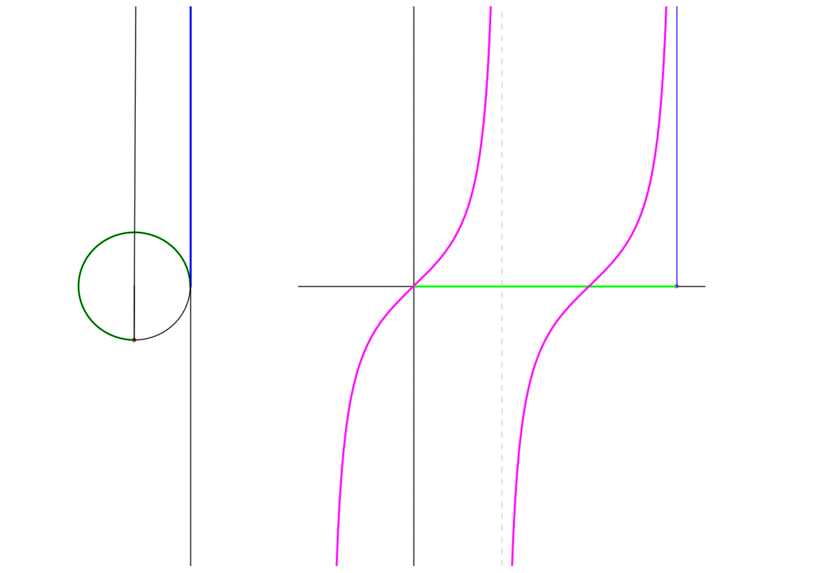
Figure 3: The tangent of a point moving in a circle

Notice that at $\theta = \dfrac{\pi}{2}$ the radius is actually parallel to the tangent and therefore $\tan \dfrac{\pi}{2}$ is undefined. Similarly for $\theta = \dfrac{3\pi}{2}$. Furthermore we see that as $\theta \to \dfrac{\pi}{2}^{-}$, $\tan \theta \to \infty$ while $\theta \to \dfrac{\pi}{2}^{+}$, $\tan \theta \to -\infty$.

Secant

$\sec \theta$ is the signed distance of the origin and interscetion of the radius through the endpoint and the line tangent to the circle at the point $(0,1)$. The following animation shows the graph traced as the endpoint traverses the unit circle:

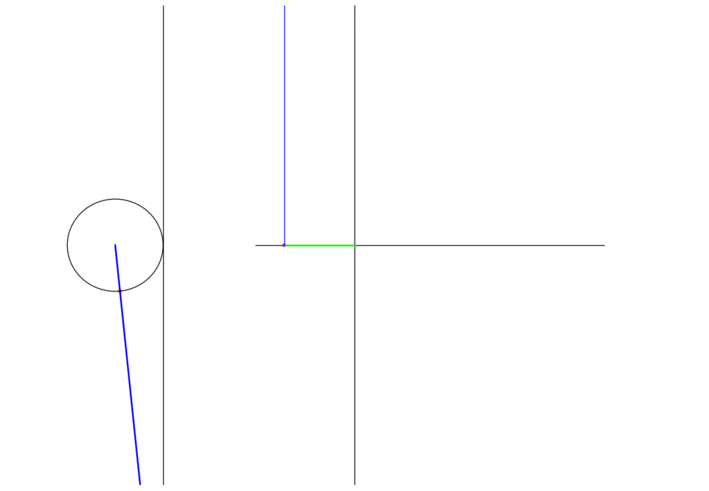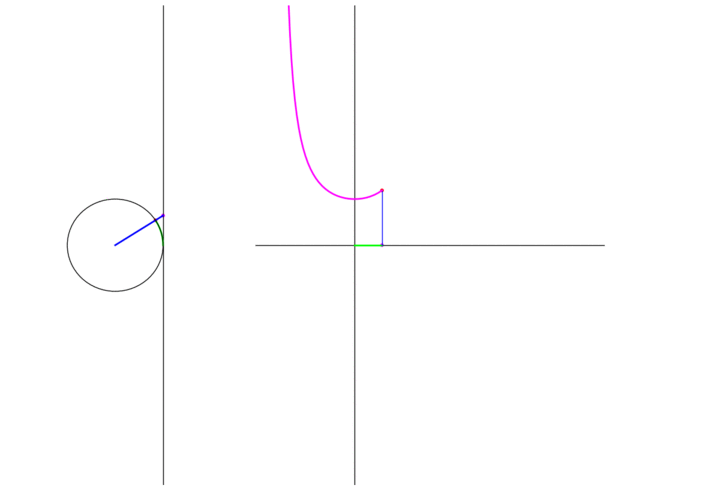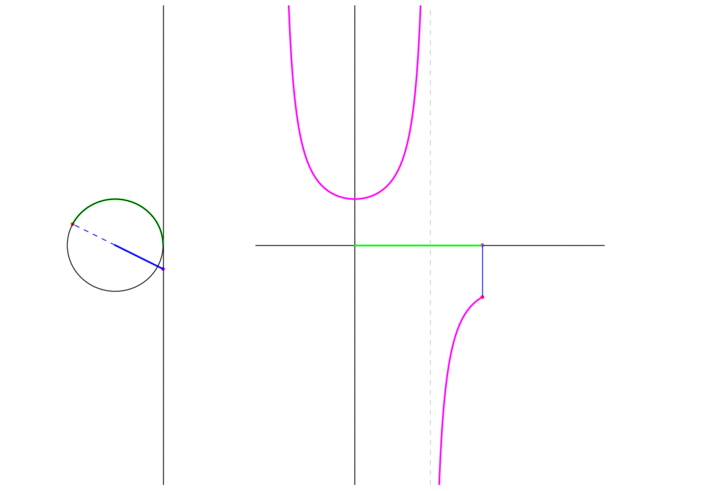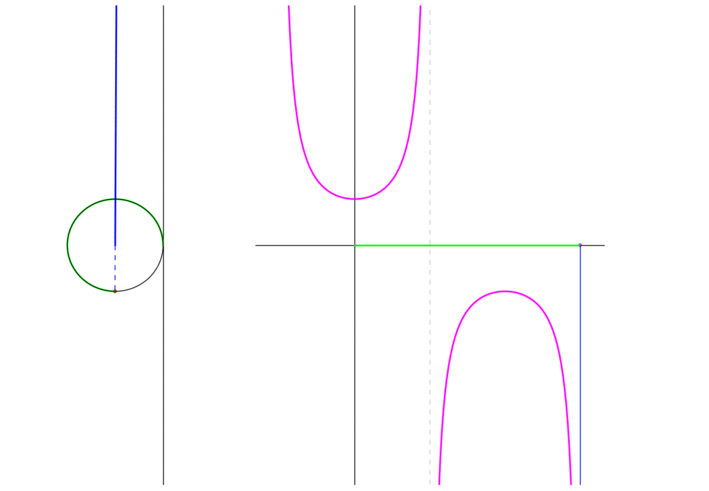
Figure 4: The secant of a point moving in a circle

Notice that at $\theta = \dfrac{\pi}{2}$ the radius is actually parallel to the tangent and therefore $\sec \dfrac{\pi}{2}$ is undefined. Similarly for $\theta = \dfrac{3\pi}{2}$. Furthermore we see that as $\theta \to \dfrac{\pi}{2}^{-}$, $\sec \theta \to \infty$ while $\theta \to \dfrac{\pi}{2}^{+}$, $\sec \theta \to -\infty$.

Cotangent

$\cot \theta$ is the signed distance of interscetion of the radius through the endpoint and the line tangent to the circle at the point $(1,0)$. The following animation shows the graph traced as the endpoint traverses the unit circle:

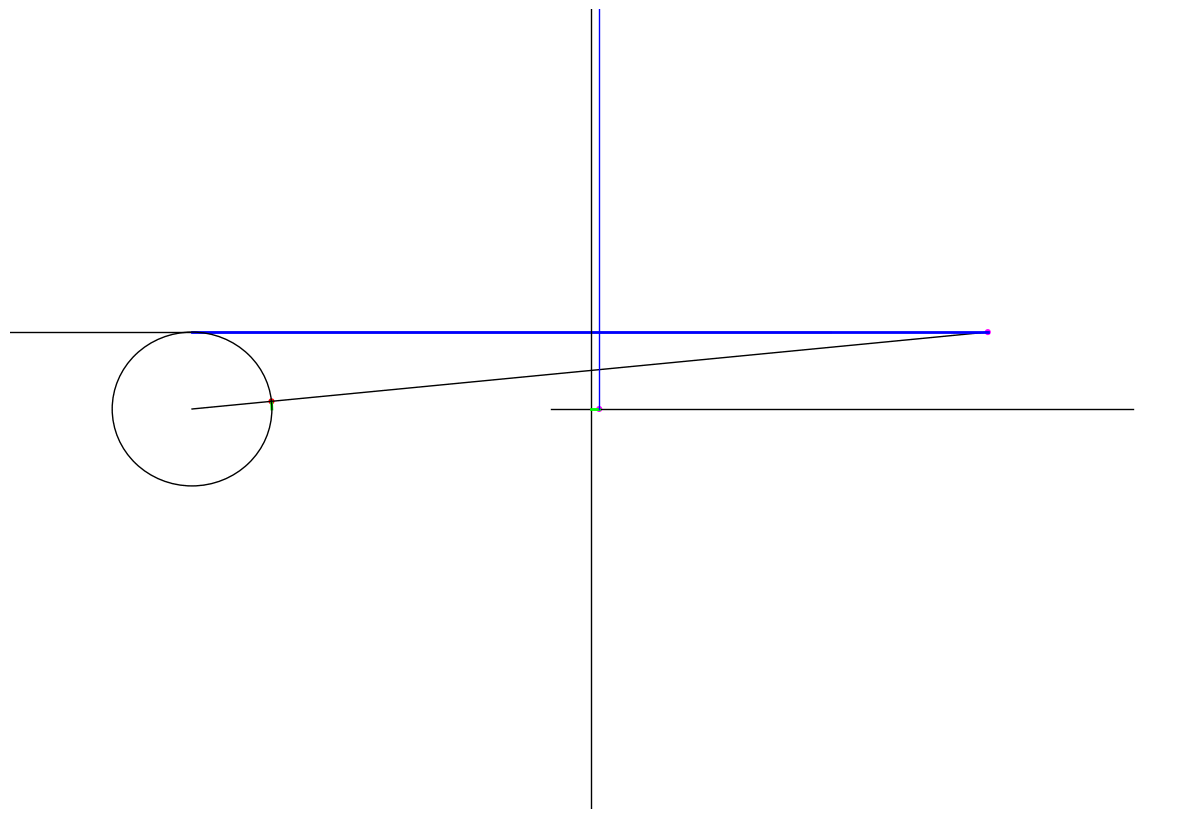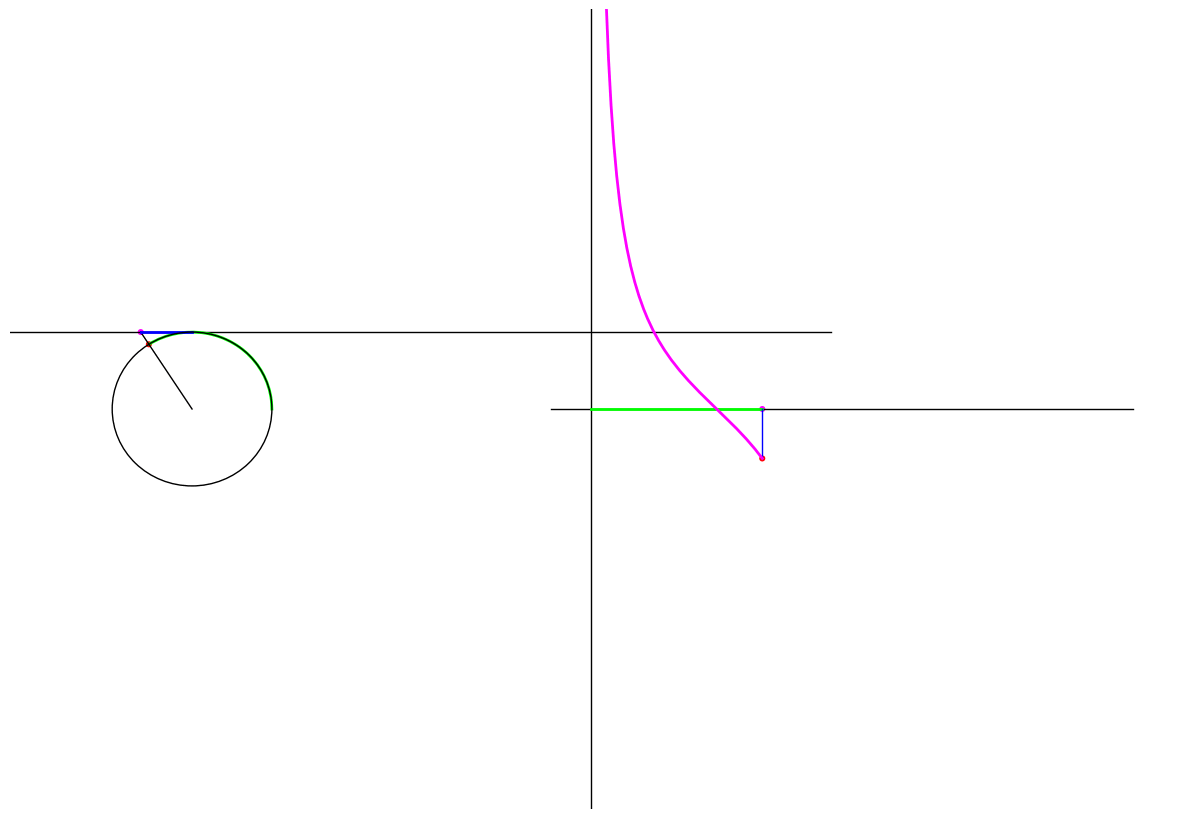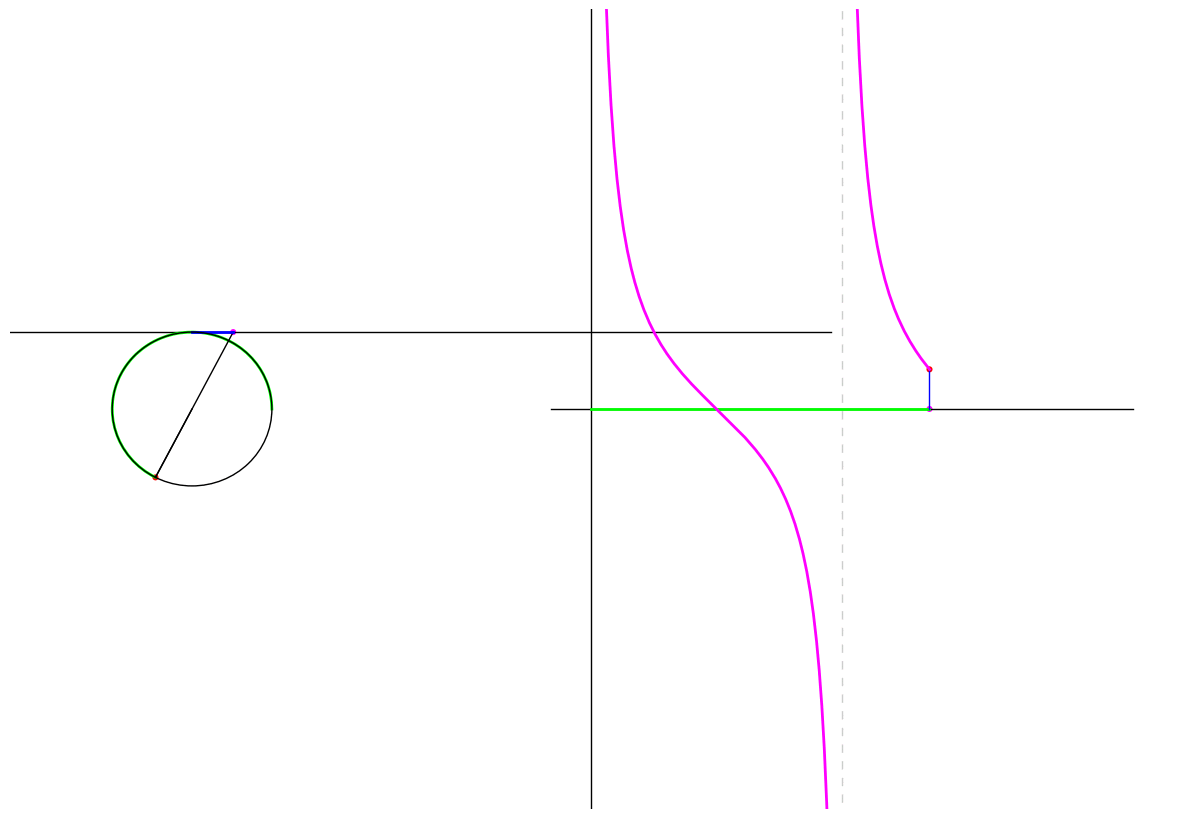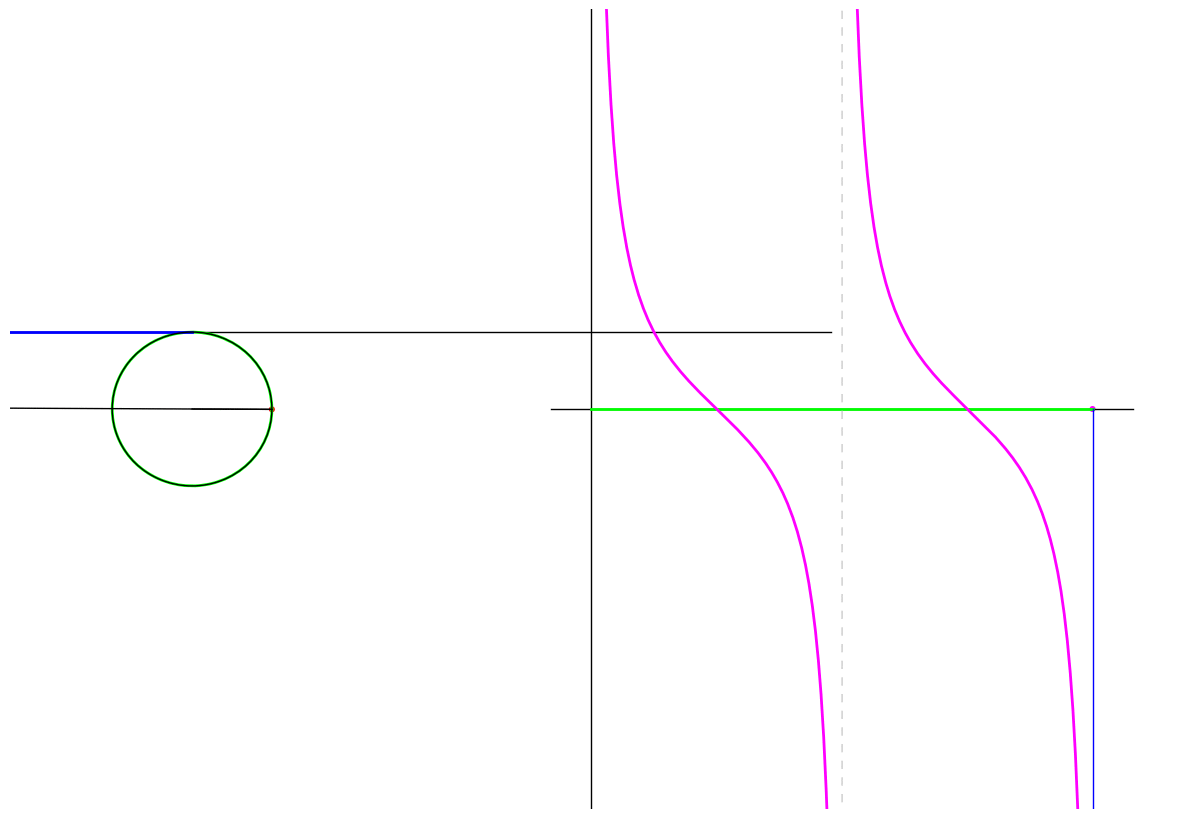
Figure 5: The cotangent of a point moving in a circle

Notice that at $\theta = 0$ the radius is actually parallel to the tangent line and therefore $\cot 0$ is undefined. Similarly for $\theta = \pi$. Furthermore we see that as $\theta \to \pi^{-}$, $\cot \theta \to -\infty$ while $\theta \to \pi^{+}$, $\cot \theta \to \infty$.